La física es una ciencia fascinante que estudia las propiedades de la Materia y la Energía, como también establece las leyes que explican los fenómenos naturales. Hoy en día y desde hace un tiempo, resulta de gran interés llevar a cabo el modelado y la simulación de los procesos físicos a fin de poder predecir el comportamiento de un fenómeno.

Las ecuaciones diferenciales son las que mejor se acercan a la descripción de la realidad en un fenómeno físico. A partir de ellas se pueden llegar a conclusiones y modelos matemáticos para modelar y simular dichos fenómenos.

La Física de Reactores o la Cinética de Reactores Nucleares presentan un gran atractivo en los procesos que en ella se producen, y modelar su comportamiento es fascinante.

La cinética de un reactor nuclear está definida con las “Ecuaciones de la Cinética Puntual” que son nada menos que un sistema de 7 (siete) ecuaciones diferenciales de primer orden a variables separables explicitadas en la figura 1. Pero para simplificar el cálculo analítico y computacional se utiliza la “Teoría de un solo grupo de neutrones” postulado por Glasstone y Sesonske (1968).

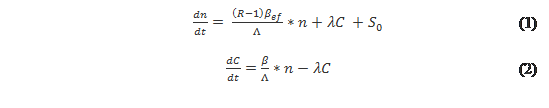Figura 1. Ecuaciones de la cinética puntual siguiendo la Teoría de un solo grupo.

Este sistema de ecuaciones es un sistema acoplado donde la población de neutrones (n) genera los neutrones precursores (C) y viceversa. Además se cuenta con un término fuente (So) que genera una población inicial. Por otro lado aparece el término reactividad (R) asociado al control del reactor. También tenemos la velocidad total de formación de neutrones retardados iCi.

Las herramientas computacionales permiten el desarrollo de la simulación pero es indispensable entender la matemática a modelar ya que de ella dependen los resultados.

La simulación del comportamiento de la población neutrónica en MATLAB como herramienta computacional dentro del entorno de Simulink, permite analizar los parámetros físicos de un reactor y reproducir el comportamiento de la población neutrónica de un reactor nuclear definiendo cada uno de los estados posibles del mismo: Subcrítico – Crítico – Supercrítico como vemos en las figuras 2, 3 y 4 respectivamente

 

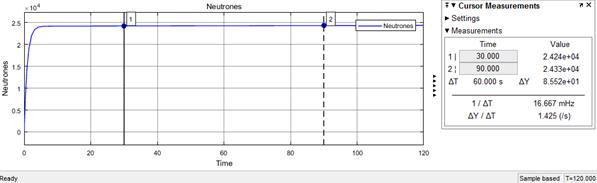Figura 2.  Gráfica del crecimiento de la población neutrónica caracterizando el estado Subcrítico (R < 0). Vemos que el crecimiento de la población neutrónica en un principio es rápido y luego crece lentamente, como lo expresan las mediciones insertadas en la gráfica.

Figura 3. Gráfica del crecimiento de la población neutrónica caracterizando el estado Crítico (R = 0). Vemos que el crecimiento de la población neutrónica en un principio es rápido y luego crece de forma lineal, como lo expresan las mediciones insertadas en la gráfica.

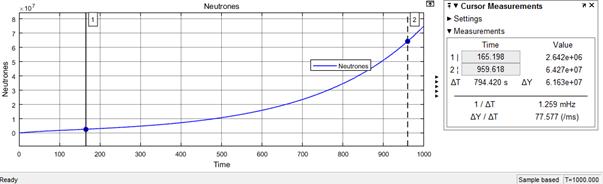Figura 4. Gráfica del crecimiento de la población neutrónica caracterizando el estado Supercrítico (0 < R <1). Vemos que el crecimiento de la población neutrónica tiene forma exponencial.

Se logra modelar el crecimiento de la población neutrónica con un solo grupo de neutrones. Si bien es cierto ya existen códigos neutrónicos para el modelado del comportamiento de la población neutrónica, pero dentro de un marco de seguridad nuclear donde se requiere altísima precisión y definición en los métodos numéricos utilizados. Este desarrollo encuadra dentro de un carácter didáctico en Simulink y no deja de ser un aporte valioso para la enseñanza de la física de reactores de forma sencilla, versátil y de interface amigable para la presentación e interpretación de los datos y curvas características

M. Sc. Ing. David Martín Eduardo Almaraz