Por la diversidad de tareas que se realizan cotidianamente en la ingeniería, los ingenieros nos alejamos de los principios físicos básicos que se estudian durante el cursado de la carrera de grado, se comienzan a tratar temas en forma exageradamente práctica, como consecuencia,  aquellos conceptos aprendidos en nuestros años de estudiante se vuelven difusos con el transcurrir del tiempo.

Un ejemplo, se puede encontrar en la respuesta que se recibiría si nos preguntan: ¿Cuál es la velocidad con que se desplazan los electrones en un conductor?

Es usual escuchar como respuesta: “un poco menos que la velocidad de la luz, considerando que cuando encendemos una lámpara el efecto es instantáneo”.

Suponiendo que la respuesta es correcta, se hará una análisis teórico/práctico para tratar de demostrar su veracidad. Para esto tendremos que regresar en el tiempo a nuestra vida de estudiante, sin conocimientos prácticos de la ingeniería, pero con mucho entusiasmo y entrenamiento para razonar, los que posiblemente se vieron disminuidos con el pasar de los años.

Considerando como cierta la respuesta, asumimos que los electrones se desplazan con una velocidad  relativamente menor a la correspondiente de la luz, por ejemplo  v= 250.000 km/s  (c≈300.000 km/s).

Ahora bien, nos preguntemos: ¿Qué efectos produciría esta velocidad sobre el conductor?

Para dar una respuesta tendremos que traer a colación ciertos conceptos básicos, estudiados durante la carrera, que nos permitirán  interpretar estos efectos.

Se define como cuerpo conductor, aquel que posee electrones libres y se designa con el símbolo “n” a la cantidad de cargas libres por unidad de volumen que el cuerpo conductor posee.

Los metales se caracterizan por tener una importante cantidad de electrones libres, lo cual los convierte en buenos conductores. Por ejemplo el cobre tiene  8,45×10²²  electrones libres /cm³, en cambio la plata tiene 5,86 x10²²  electrones libres /cm³.

Comenzaremos el análisis considerando que el conductor es parte de un circuito de corriente continua.

 

Si realizamos un corte perpendicular en este conductor, visualizaremos la sección transversal del mismo. Esta sección es atravesada por electrones en movimiento o sea que pasa una determinada  carga eléctrica por unidad de tiempo, que se la llama intensidad de  corriente eléctrica cuya unidad es Ampere (Coulomb/s).

Si relacionamos esta corriente con la sección transversal obtendremos la densidad de corriente en A/mm² designada con el símbolo “J”.

La  velocidad “v” con que se mueven las cargas que originan la corriente se llama velocidad de arrastre de las cargas libres. Dicha velocidad es la que se supone, erróneamente, aproximada a la velocidad de la luz.

Ahora bien, ya aclarado esta serie de conceptos, comencemos con el análisis teórico/práctico de lo planteado anteriormente.

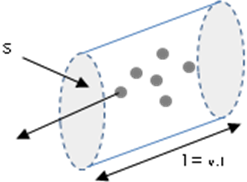
Consideremos un sector de conductor cuya longitud sea la distancia recorrida por los electrones en un segundo, este sector será un cilindro siendo una de las bases la sección transversal “S” que será atravesada por los electrones contenidos en ese cilindro en el próximo segundo.

Si tomamos como longitud del cilindro la distancia recorrida por los electrones a una velocidad “v” en un segundo, esto es l=v.t  (longitud o altura del cilindro).

Para conocer la cantidad de electrones libres que contiene el cilindro, tendremos que calcular el volumen de este y multiplicarlo por la densidad de electrones libres del metal con el que está constituido dicho conductor.

Volumen = área x altura = S.l = S.v.t (para t=1 segundo)

Volumen = S.v.t [cm³]

La cantidad de electrones libres en este volumen será  (S.v.t.n) si a esta cantidad la multiplicamos por el valor absoluto de la carga de cada electrón  e^– = 1,602x 10^{-19C ,} obtendremos la carga total contenida en ese cilindro, la cual en el próximo segundo, atravesará la sección transversal del conductor.

Q = carga contenida en el cilindro = S.v.t.n.e^–  [Coulomb]

Si  dividimos por el tiempo  obtendremos la corriente eléctrica, cuya unidad es el Ampere o Coulomb por segundo.

I = Q/t = S.v.n.e^– [C/s]

Si la dividimos por la sección obtendremos la densidad de corriente, cuya unidad será  Ampere por mm².

J = I/S = e^–.n.v [A/mm²]

Realicemos con esta sencilla ecuación, que pueden encontrar en cualquier libro de Física, el primer ejercicio para verificar la veracidad de la afirmación inicial. Utilizaremos un conductor de cobre.

J = 1,602×10^-19 C x 8,45×10²² electrones/cm³ x 25×10⁹ cm/s

J = 338,42×10¹²  [C/s.cm²]

J = 338,42×10¹² [A/cm²] = 338,42×10¹⁰ [A/mm²]

Si observamos el resultado, inmediatamente notaremos  que  la densidad de corriente en el conductor es inconsistente con la realidad, ya que lo volatilizaría en un instante, razón por la cual comenzamos a dudar de la afirmación.

Continuando con otro ejemplo, relacionado con una práctica habitual en una instalación eléctrica, estamos hablando de una instalación de cables sobre bandejas.

Cuando en una instalación industrial se instala un cable del tipo subterráneo en una bandeja, se tiene la precaución, en los cambios de dirección, de respetar el radio mínimo de curvatura determinado por el fabricante.

Para el ejemplo se considera un cable subterráneo unipolar de 150 mm² de cobre aislación 1kV sin armadura y sin blindaje, cuyo radio mínimo de curvatura determinado por el fabricante es de r = 28 cm.

Al encontrarse los electrones con una velocidad en el cable de  250.000 km/s, para cambiarles la dirección lineal de la velocidad en una curva, se necesita una cierta fuerza centrípeta, ya que por más pequeños que sean poseen una cierta masa (m_e= 9,108 x 10^-31 kg). Esta fuerza se pone de manifiesto en la curva sobre la estructura del conductor, dicho esfuerzo se transmitirá desde el conductor directamente a la bandeja.

Fc = fuerza centrípeta = m_e.a_c  (por electrón)

m_e = masa electrón               a_c= aceleración centrípeta = v²/r            r = radio de curvatura

Fc = m_e.v²/r     Si consideramos todos los electrones contenidos en el volumen de estudio ó cilindro, tendremos la fuerza centrípeta total:

∑Fc=  ( m_e.v²/r).S.v.t.n          l=v.t

Si calculamos la fuerza total por unidad de longitud

Fct=  ( m_e.v²/r).S.v.t.n/v.t

Fct=  ( m_e.v²/r).S.n [N/m]

Fct=  2,58 x 10⁹  [N/m]                       Fct=  263  [ t/mm ]

Sería imposible que el cable soporte este esfuerzo por milímetro de longitud en la curva.

Una situación similar se presentaría en una línea aérea debido a la forma de la  catenaria, la fuerza centrípeta  significaría aumentar varias veces el peso del conductor, si es que se supone que lo electrones se desplazaran a dicha velocidad.

Los ejemplos propuestos demuestran la inconsistencia de la velocidad supuesta, razón por la cual plantearemos en forma inversa el problema y comenzaremos aceptando la densidad de corriente sugerida por el fabricante para que el conductor de cobre no supere la temperatura que soporta el aislante.

Para determinadas  condiciones de instalación, el fabricante determina para un cable subterráneo de cobre de 150mm2 de sección transversal  para 1kV de aislación, una intensidad de corriente de 420A.

Utilizando la ecuación de densidad de corriente obtenida anteriormente:

J = I/S = e^–.n.v [A/mm²]

J = 420/150 [A/mm²]             J = 2,8 [A/mm²]

Si despejamos la velocidad de arrastre de los electrones y la calculamos:

v=  J/(e^–.n)  [m/s]                      v=  2,07 x 10^-4   [m/s]                   v=  74,5  [cm/h]

Este resultado corresponde  a corriente continua y se concluye que la velocidad de los electrones en el conductor es directamente proporcional a la densidad de corriente e inversamente proporcional a la densidad de electrones libres.

Se puede apreciar que la velocidad de arrastre es extremadamente baja y esto desestima la veracidad de la afirmación inicial.

Si verificamos la fuerza total sobre la estructura del cable de 150mm² considerando la velocidad de arrastre real será:

Fct=  1,76x 10^-15  [N/m]     (valor despreciable)

 

A continuación analizaremos el movimiento de los electrones en corriente alterna sinusoidal que posiblemente sea menos conocido y más difícil  de interpretar.

En la ecuación de  velocidad de arrastre, la carga del electrón y la densidad de cargas libres las consideramos constantes para un determinado material, y es la densidad de corriente la que seguirá  la ley de variación de la tensión de fuente. Por lo tanto la velocidad de los electrones también acompañará esta variación, consideremos que es una función sinusoidal:

v=  J/(e^–.n)  [m/s]                              J(t)= J_max   senwt

v(t)=(J_max/e^–.n)  senwt   v(t)= V_max   senwt

V_max = J_max/e^–.n (valor máximo de la velocidad)

Para calcular el desplazamiento de cada electrón tendremos que integrar el producto de la velocidad por el tiempo.

x(t)=  ʃv(t)dt=  ʃ V_max   senwt dt

x(t)= – ( J_max/e^–.n.w) coswt

x(t)= – X_max coswt

Siendo X_max  la amplitud del desplazamiento del electrón con respecto a una posición central.

X_max = J_max/e^–.n.w

Si realizamos el cálculo  para  una frecuencia de 50 Hz, tendríamos:

w=   2πf =  314  [s^-1]

La densidad de corriente eficaz para el conductor del ejemplo es :

J = 2,8 [A/mm²]             por lo tanto el valor máximo será   J_max = √2 J =  3,96 [A/mm²]

X_max = 0,93 µm

Esto significa que los electrones en un sistema de corriente alterna de 50Hz no se desplazan solo vibran con respecto a una posición central, que para nuestro ejemplo de un cable de cobre con una densidad de corriente eficaz de 2,8 A/mm² el desplazamiento máximo que experimentan es de 0,93micometro.

Es por esta razón que podríamos llamar a los electrones de nuestra instalación “amigos y colaboradores” ya que permanecen sin moverse de su lugar de trabajo a lo largo de toda  la vida de la instalación.

Este artículo, no pretende ser un artículo científico su finalidad es explicar en forma sencilla algunos conceptos que posiblemente hayamos olvidado o que se estudiaron sin la profundidad necesaria.

 

Fuente : Libro de Física – Raymond A. Serway

Por: Ing. Carlos E. Ferrari

Gerente Técnico y de Desarrollo de Electroingeniería I.C.S.S.A